8. Using R as a graphing calculator

In my first R tutorial, I showed you how to use R as a simple calculator. Now let’s step things up by using R as a graphing calculator. I assume here that you know how to open the R console. If you don’t know how to do that, see the first tutorial.

Plotting a parabola

The way I learn to program is by first having something I want to do, and then by figuring out how to do it. So let’s start with what we want to achieve. We want to plot a simple parabola, defined by the equation y = x² .

How do we do that?

Variables

Our first step will be to see how variables work in R. In the equation for our parabola, we have two variables: x and y.

In R, you can define a variable just like you would in algebra. To define a variable called x that is equal to 5, I type x = 5 and press enter:

x = 5

If all goes well, nothing will happen. That’s right, R does not tell you when it has successfully stored a variable. (Side note: this is one reason many people use R with an IDE (integrated development environment) like Rstudio. The IDE will show you the variables you have stored.)

To check our variable, we can type x into the console and press enter. We get back the value we defined:

> x
[1] 5

Another note. In addition to using the = sign to define values, in R you can also use the <- symbol, which is supposed to represent an arrow going into the variable:

x <- 5

I’m going to be honest; I never use this notation. I find it ugly, and it’s not how other computer languages work. And so I always define variables using the = sign.

Back to our parabola, which is defined by the equation y = x² .

In R, we’ve already defined x. So let’s now define y. Type the following into your console and press enter:

y = x^2

Again, if all goes well, R will remain silent. We can check that our y-value is stored correctly by typing y and pressing enter:

> y
[1] 25

Remember that we defined x = 5. So it seems that y has the correct value, since 5² = 25.

What we’ve got right now is a single point on the x-y coordinate plane; the point (x = 5, y = 25). To make our parabola, we need many more points. But how do we do that?

Vectors

Here’s where ‘vectors’ come in. In R, a ‘vector’ is just a variable that holds multiple values. In other languages, this type of object is called an ‘array’ or a ’list’. But remember that R thinks like a mathematician. And to mathematicians, a list of values is called a ‘vector’.

Here’s how it works. Suppose I want to list all the numbers between 1 and 10. R has a nice notation for achieving this. We use the : symbol. To list the numbers from 1 to 10, we type 1:10 and press enter:

> 1:10
 [1]  1  2  3  4  5  6  7  8  9 10

R automatically prints all the integers between 1 and 10. Nice!

I suggest playing around with this feature to get a sense for how it works. For example, you don’t have to start at the number 1. You can start at 5:

> 5:10
[1]  5  6  7  8  9 10

And you can go higher (or lower) than 10. Here’s up to 20:

> 5:20
 [1]  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20

Once you’re comfy with this notation, realize that you can use it to define a variable. For example, we can dump the numbers from 1 to 10 into the variable x:

x = 1:10

Again, if all goes well, R will remain silent. But you can check your variable by typing it into the console:

> x
 [1]  1  2  3  4  5  6  7  8  9 10

We’re getting closer to our parabola! Now let’s define the variable y as the square of x:

y = x^2

Here’s what R has stored for y:

> y
 [1]   1   4   9  16  25  36  49  64  81 100

Everything looks good.

The plot function

So far we’ve got a list of values for x and y. To get a parabola, we need to plot these values on the x-y coordinate plane. We do that using the plot function. This function takes x and y values, and plots them on a coordinate plane:

plot( x, y )

Here’s what I get back:

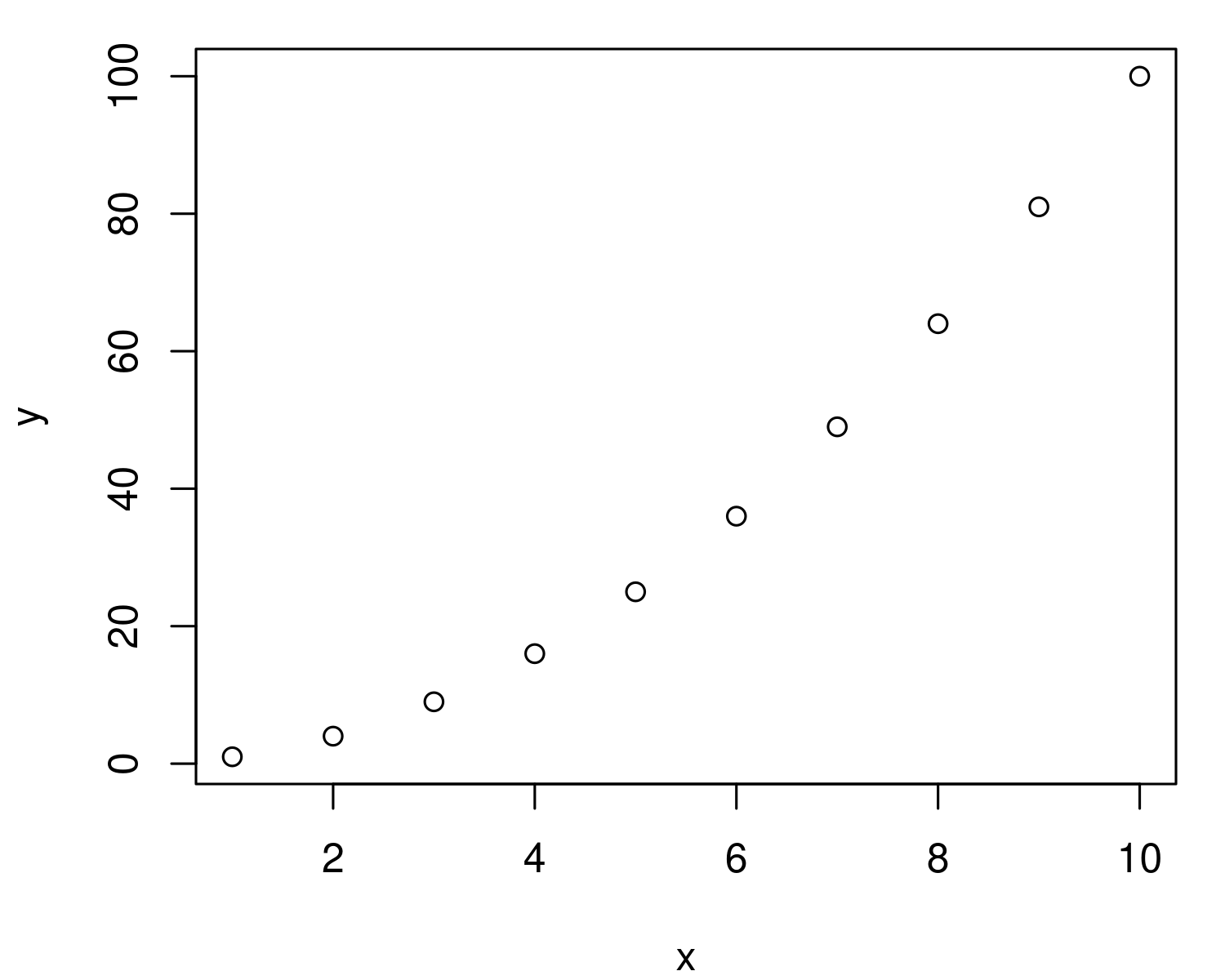
Alright, we’re getting close to our parabola. We just need to pick better values for x.

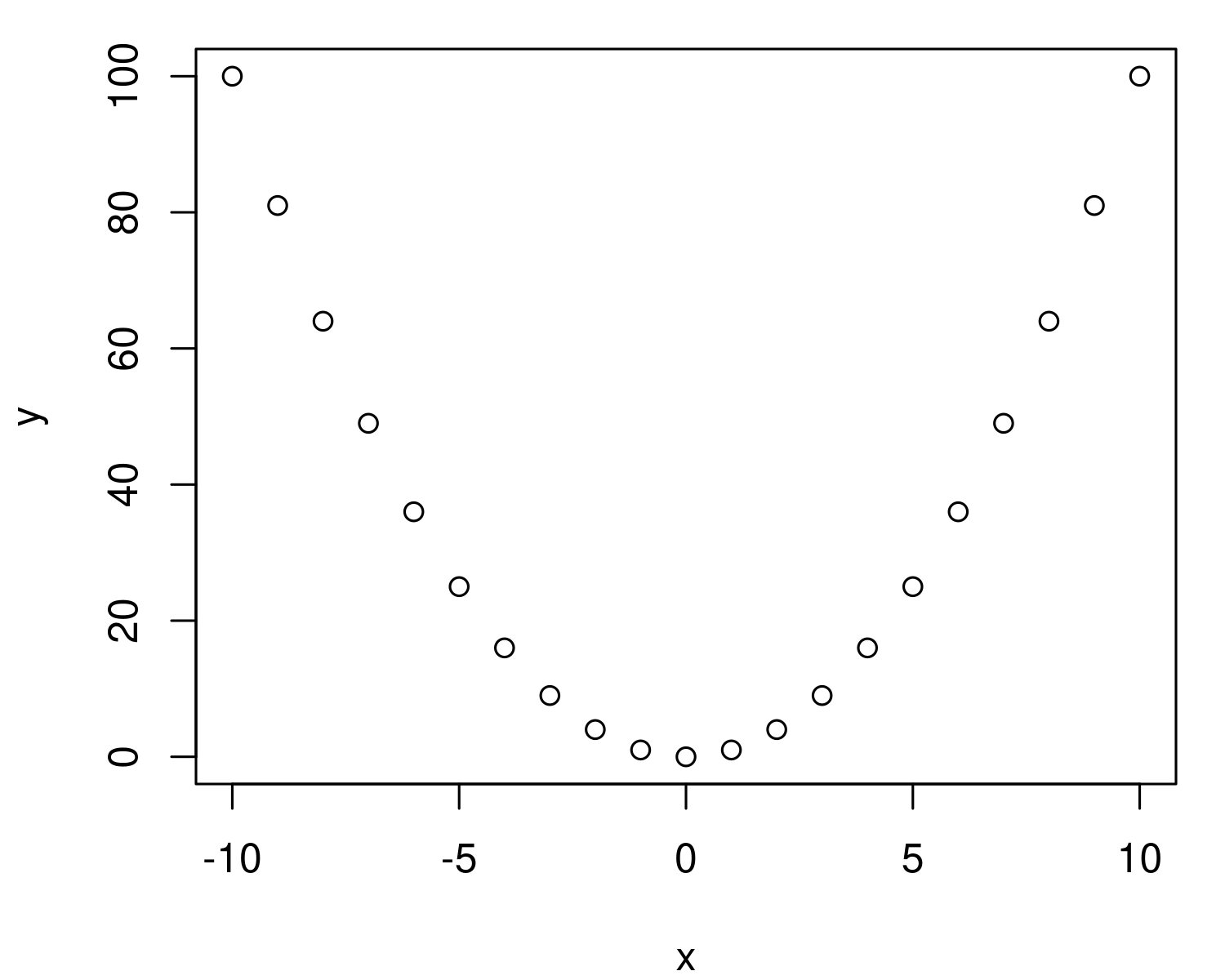
Let’s define x to go from -10 to 10:

x = -10:10

Now let’s use these values to define y:

y = x^2

And finally, plot the values:

plot(x, y)

Presto! We’ve got a parabola:

By default, R’s plot function will plot points. But our parabola will look prettier if we use a line. We can do that by telling the plot function to use type = "l":

plot( x, y, type = "l")

And now we get a very pretty parabola:

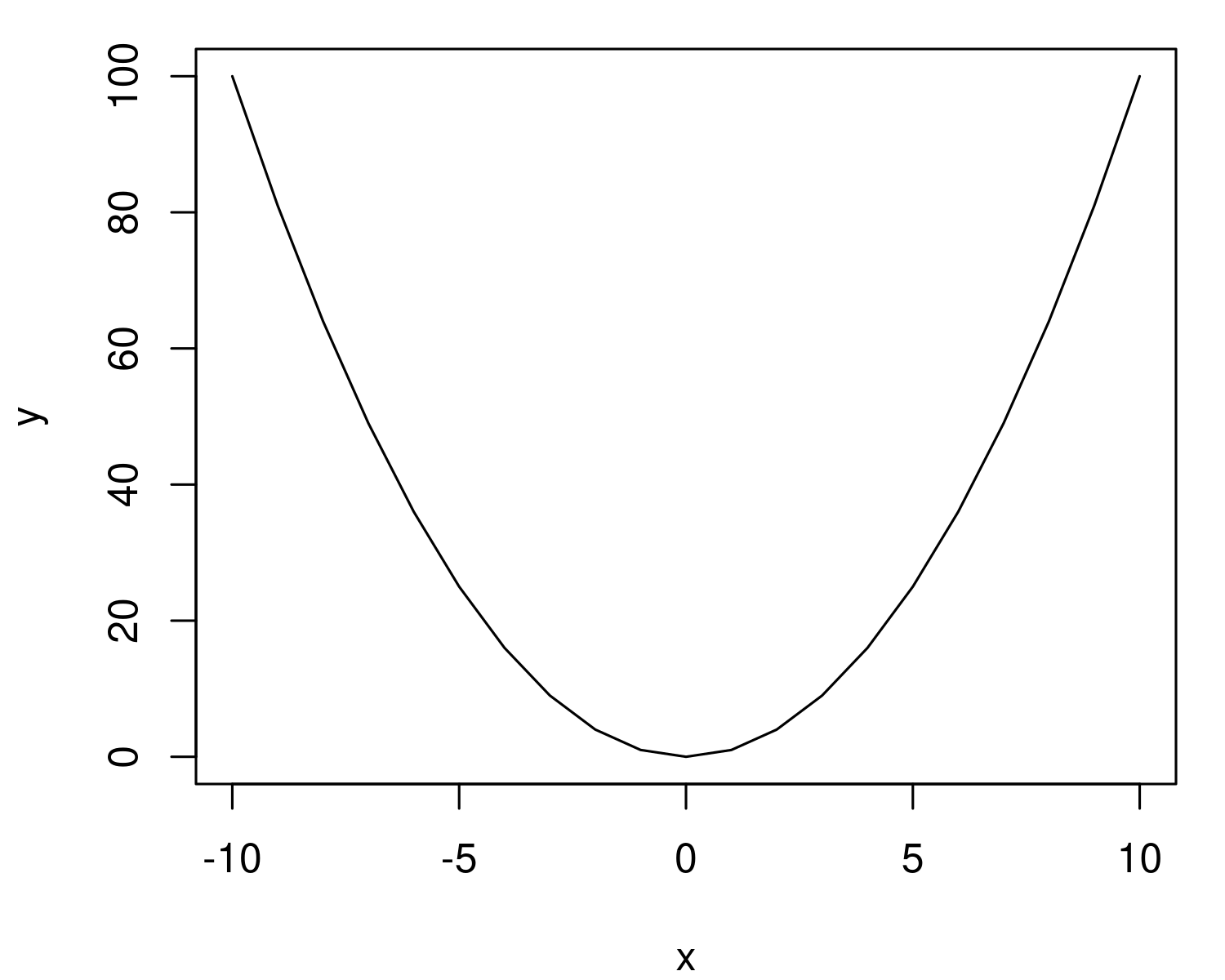
If you’ve gotten this far, try plotting a slightly different function.

For example, y = 2 x² .

First, define the range for your variable x. The define y as:

y = 2*x^2

Or how about y = x² - 2:

y = x^2 - 2

Remember that the best way to learn R is to experiment. Happy plotting!